Universal Law of Gravitation

A mass is at the centre of a square, with four masses at the corners as shown: 

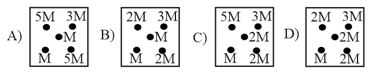
Rank the choice according to the magnitude of the gravitational force of the center mass. 

The gravitational force in a region is given by, $\overrightarrow{F}=m\left(ay\hat{i}+ax\hat{j}\right)$. The work done by gravitational force to shift a point mass $m$ from$(0,0,0) to (x_0,y_0,z_0)$ is

A projectile is launched from the surface of the earth with a very high speed $v$ at an angle $\theta$ with vertical. What is its velocity when it is at the farthest distance from the earth surface, given that the maximum height reached by the projectile is equal to the height reached when it is launched perpendicular to earth with a velocity=$\sqrt{\frac{GM}{R}}$

Why gravitational force of Earth exerts centripetal force on satellite? Why does the Earth not attract the satellite to collide?

Two identical particles each of mass $m$, move in circular path due to their own mutual gravitational force. Find the velocity of the particle if the radius of the circular path is $a$.

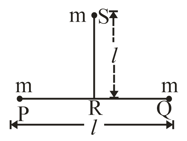
Two particles each of mass$m$are placed at points $P$ and $Q$ as shown in the figure. $R$ is the mid point of PQ=$l$. The gravitational force on the third particle of mass $m$ placed at point $S$ on the perpendicular bisector of $PQ$ at distance from R is:-

Consider a ring of mass $m$ and radius $r$. Maximum gravitational intensity on the axis of the ring has value

How far from earth must a body be along a line towards the sun so that the sun's gravitational pull on it balances that of the earth. Distance between sun and earth's centre is $1.5\times {10}^{10}\mathrm{}\mathrm{k}\mathrm{m}$. Mass of sun is $3.24\times {10}^5$ times mass of earth.

Two particles of mass$M$  exert a force $F$ on each other. If $50\%$ of mass is transferred from one to other. The force between them is changed by

Find the value of the gravitational constant in CGS system.

Three particles, each of mass $M$, situated at the vertices of an equilateral triangle of side length $L$. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original separation $L$. The initial speed that should be given to each particle is

$Titan\left(M=3\times {10}^{18} \mathrm{kg}\right)$ is revolving a star in an orbit of radius $\left(2\times {10}^7\right) \mathrm{km}$ with angular velocity $\left(9\times {10}^{-7}\right) \mathrm{rad} {\sec }^{-1}$. The force (in Newton) exerted on titan will be

Two small solid spheres each of mass $m=1 \mathrm{kg}$ are thrown at the same time with same initial velocity $v=200\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$ and angle $\theta =30°$ with the horizontal. Sphere $2$ is thrown at a height $h=1 \mathrm{m}$ above sphere $1$ as shown in the figure. Counting the gravitational force between the two spheres, calculate the change of distance $\delta h\left(\times {10}^{-8} \mathrm{m}\right)$ between the two spheres, at the moment sphere $1$ hits the ground. You may take the distance between the two spheres as constant $h$ in your derivation for the gravitational force because $\delta h\ll h$.

$\left(G=\frac{20}{3}\times {10}^{-11} \mathrm{N} {\mathrm{m}}^2 {\mathrm{kg}}^{-2} \text{and} g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

When two mass electron are placed at a distance of $9\mathrm{cm}$, calculate force on another proton placed at a distance of $9\mathrm{cm}$ from electron?

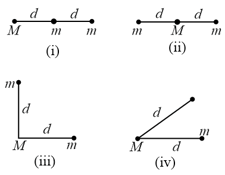
Three particles, two with masses $m$ and one with mass $M$, might be arranged in any of the four configurations shown below. Rank the configurations according to the magnitude of the gravitational force on $M$, least to greatest

Two particles of masses $4\mathrm{kg}$ and $8\mathrm{kg}$ are kept at $x=-2 \mathrm{m}$ and $x=4 \mathrm{m}$ respectively. Then the magnitude of net gravitational force acting on a third particle of mass $1\mathrm{kg}$ kept at the origin is

Two identical particles of combined mass $\mathrm{M}$, placed in space with certain separation, are released. Interaction between the particles is only of gravitational in nature and there is no external force present. Acceleration of one particle with respect to the other when separation between them is $\mathrm{R}$, has a magnitude:

What is earth's mass?

Consider a universe with modified electrostatics where like charges attract and unlike charges repel. Three positively charged point particles with same charge to mass ratio $\alpha$ interact with each other through the electrostatic force. Total mass of the system is $M$. The system can move about it's centre of mass with equal distances between all pairs of masses. When the masses are separated by a distance $d$, the angular frequency of the motion about the centre of the mass is

Why earth is rotating ?